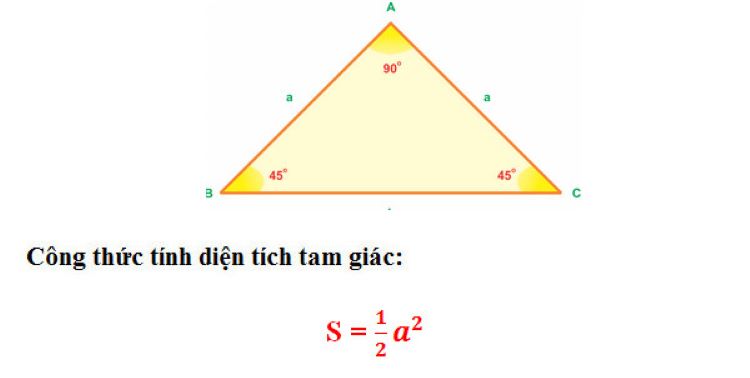
Diện tích tam giác vuông cân
Tam giác vuông cân là một tam giác đặc biệt trong hình học, có một góc vuông (90 độ) và hai cạnh góc vuông bằng nhau. Nói cách khác, đây là tam giác vừa có tính chất của tam giác vuông (một góc bằng 90 độ) vừa có tính chất của tam giác cân (hai cạnh bằng nhau). Trong tam giác vuông cân, hai góc nhọn còn lại luôn bằng nhau và mỗi góc có số đo là 45 độ. Tam giác này thường xuất hiện trong các bài toán hình học cơ bản vì có tính đối xứng và dễ tính toán.
Với tam giác vuông cân có hai cạnh góc vuông bằng nhau và gọi độ dài mỗi cạnh là a, ta có công thức tính diện tích:
Diện tích = (1/2) × a × a = (a²) / 2
Bài tập áp dụng
Bài 1:
Cho tam giác vuông cân có độ dài cạnh góc vuông là 6 cm. Tính diện tích tam giác đó.
Lời giải:
Áp dụng công thức:
Diện tích = (1/2) × 6 × 6 = 36 / 2 = 18 cm²
Đáp án: 18 cm²
Bài 2:
Tính diện tích tam giác vuông cân nếu cạnh góc vuông của tam giác đó có độ dài là 8 cm.
Lời giải:
Áp dụng công thức:
Diện tích = (1/2) × 8 × 8 = 64 / 2 = 32 cm²
Đáp án: 32 cm²
Bài 3:
Một tam giác vuông cân có cạnh góc vuông dài 10 cm. Tính diện tích của tam giác.
Lời giải:
Áp dụng công thức:
Diện tích = (1/2) × 10 × 10 = 100 / 2 = 50 cm²
Đáp án: 50 cm²
Công thức tính diện tích tam giácBài 4:
Tính diện tích tam giác vuông cân có độ dài cạnh góc vuông là 12 cm.
Lời giải:
Áp dụng công thức:
Diện tích = (1/2) × 12 × 12 = 144 / 2 = 72 cm²
Đáp án: 72 cm²
Tam giác vuông cân là một loại tam giác đặc biệt trong hình học, vừa có tính chất của tam giác vuông (một góc vuông 90 độ) và vừa có tính chất của tam giác cân (hai cạnh góc vuông bằng nhau). Dưới đây là một số tính chất hình học quan trọng của tam giác vuông cân:
Hai cạnh góc vuông bằng nhau
Trong tam giác vuông cân, hai cạnh góc vuông luôn có độ dài bằng nhau. Nếu gọi độ dài của mỗi cạnh góc vuông là a, thì ta có:
AB=AC=a
(với tam giác vuông cân ABC vuông tại A).
Cạnh huyền được tính theo định lý Pythagoras
Cạnh huyền trong tam giác vuông cân có thể tính được bằng định lý Pythagoras. Vì tam giác vuông cân có hai cạnh góc vuông bằng nhau, ta có:
BC = √(a² + a²) = √(2a²) = a√2
(với BC là cạnh huyền, a là độ dài của mỗi cạnh góc vuông).
Các bài tập áp dụngHai góc nhọn bằng nhau
Tam giác vuông cân có hai góc nhọn luôn bằng nhau. Vì tổng ba góc trong một tam giác luôn bằng 180 độ, trong đó có một góc vuông 90 độ, nên hai góc nhọn còn lại mỗi góc có độ lớn là 45 độ:
∠ABC=∠ACB=45∘
Trục đối xứng
Tam giác vuông cân có một trục đối xứng, là đường phân giác của góc vuông (góc tại A). Trục này chia tam giác thành hai phần bằng nhau.
Diện tích
Diện tích của tam giác vuông cân có thể tính dễ dàng theo công thức:
Diện tích = ½ x a x a = a² / 2
(với a là độ dài của mỗi cạnh góc vuông).
Chu vi
Chu vi của tam giác vuông cân được tính bằng tổng độ dài ba cạnh của tam giác:
Chu vi=a+a+a√2=2a+a√2

Ứng dụng của tam giác vuông cân trong thực tếỨng dụng của S tam giác vuông cân trong thực tế rất đa dạng và hữu ích trong nhiều lĩnh vực. Dưới đây là một số ứng dụng tiêu biểu của tam giác vuông cân:
Xây dựng và thiết kế kiến trúc
Tính toán diện tích mái nhà: Trong thiết kế mái nhà, mái chóp vuông cân rất phổ biến. Diện tích của mái nhà có thể được tính bằng cách sử dụng diện tích của tam giác vuông cân để xác định diện tích mái chóp hoặc mặt phẳng nghiêng.
Xây dựng bậc thang: Khi thiết kế bậc thang, các bậc có thể tạo thành một tam giác vuông cân, giúp các nhà thiết kế tính toán chính xác chiều cao và chiều rộng của từng bậc để đảm bảo sự thoải mái và an toàn cho người sử dụng.
Tính toán diện tích trong các bài toán hình học
Giải các bài toán hình học: Tam giác vuông cân thường xuất hiện trong các bài toán hình học cơ bản, giúp học sinh và sinh viên hiểu rõ hơn về mối quan hệ giữa các cạnh và góc trong tam giác vuông, cũng như áp dụng các công thức tính diện tích trong thực tế.
Kỹ thuật và công nghệ
Tính toán góc nghiêng và chiều cao: Trong một số ứng dụng kỹ thuật, chẳng hạn như xây dựng thang máy, cột đèn hoặc các cấu trúc nghiêng khác, việc sử dụng tam giác vuông cân giúp xác định góc nghiêng và chiều cao một cách chính xác.
Ứng dụng trong mô phỏng và đồ họa 3D: Trong các phần mềm mô phỏng đồ họa 3D, tam giác vuông cân là một yếu tố cơ bản khi mô phỏng các đối tượng hình học, đặc biệt là các đối tượng có đối xứng hoặc góc vuông.
Nghệ thuật và thiết kế đồ họa
Tạo ra các mô hình đối xứng: Trong nghệ thuật tạo hình, đặc biệt là thiết kế đồ họa, tam giác vuông cân có thể được sử dụng để tạo ra các mô hình hoặc họa tiết đối xứng, giúp các tác phẩm thêm phần hấp dẫn và dễ nhìn.
Trang trí nội thất: Các mẫu gạch lát sàn hoặc các yếu tố trang trí nội thất có thể được thiết kế dựa trên các hình tam giác vuông cân để tạo sự đối xứng và hài hòa trong không gian.
Dùng trong kỹ thuật đo lường
Dùng trong các công cụ đo lường: Tam giác vuông cân có thể được sử dụng trong các công cụ đo lường, chẳng hạn như thước đo góc, để xác định các góc vuông một cách chính xác.
Lĩnh vực thể thao
Tính toán quỹ đạo trong các môn thể thao: Trong các môn thể thao như bóng đá, bóng chày, tam giác vuông cân có thể được dùng để tính toán quỹ đạo hoặc góc ra sân, giúp huấn luyện viên và vận động viên hiểu rõ hơn về chiến thuật.
Thiết kế phương tiện giao thông
Tính toán khung xe và các cấu trúc hỗ trợ: Trong thiết kế khung xe, đặc biệt là các phương tiện giao thông có góc nghiêng hoặc cấu trúc tháp, tam giác vuông cân giúp tính toán và tối ưu hóa diện tích, giảm thiểu trọng lượng và tăng độ bền cho khung.
Trên đây chúng tôi đã trình bày về diện tích của tam giác vuông cân và những ứng dụng thực tế của các công thức toán học trong nhiều lĩnh vực. Hy vọng bài viết đã cung cấp cho bạn những kiến thức hữu ích và dễ hiểu về các khái niệm trong toán học.
Nếu bạn đang tìm kiếm dịch vụ đặt xe taxi sân bay giá rẻ, trọn gói, hãy liên hệ ngay với Nội Bài Vip 24/7 – chuyên cung cấp dịch vụ taxi sân bay uy tín, phục vụ nhanh chóng mọi thời điểm trong ngày.
📞 Hotline: 097.992.3336 | 0865.202.193