Bất đẳng thức cosi
Bất đẳng thức Cauchy-Schwarz (còn gọi là bất đẳng thức Cosi trong tiếng Việt) là một bất đẳng thức cơ bản và quan trọng trong toán học, đặc biệt trong lý thuyết bất đẳng thức và phân tích. Bất đẳng thức này được phát biểu lần đầu bởi Augustin-Louis Cauchy và sau đó được Hermann Amandus Schwarz mở rộng. Nó khẳng định rằng trong một không gian vector, tích vô hướng của hai vector không lớn hơn tích các chuẩn của chúng.
Hệ quả
Một số bất đẳng thức đáng nhớ
Bất đẳng thức tam giác
Nếu a, b, c là 3 cạnh trong tam giác, ta sẽ có các bất đẳng thức tam giác sau:
a > 0, b > 0, c > 0
|b – c| < a < b + c
|c – a| < b < c + a
|a – b| < c < a + b
a > b > c ⇔ A > B > C (với A, B, C lần lượt là góc đối diện cạnh a, cạnh b, cạnh c)
Bất đẳng thức là phần kiến thức cần nắm thật vững nếu các em muốn “xử đẹp” môn Toán Đại số THPT. Qua bài viết, mong rằng các em sẽ nắm vững những lý thuyết về bất đẳng thức để áp dụng giải bài tập nhanh chóng và hiệu quả.
>> Xem thêm: Diện tích tam giác vuông cân

BDT Cosi dạng tổng quát

BDT Cosi dạng đặc biệt
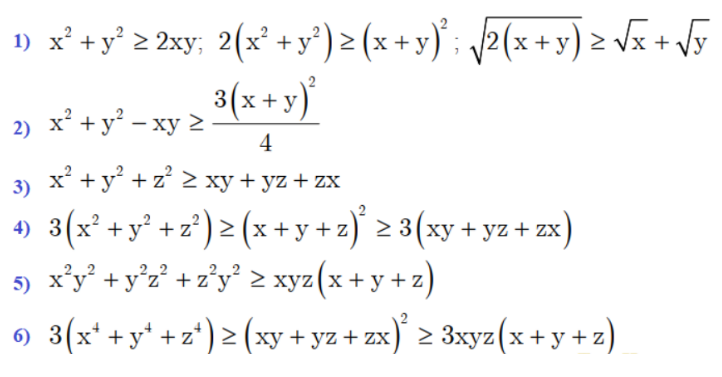
Hệ quả
Dưới đây là một số các tính chất thường gặp của bất đẳng thức:
Tính chất bắc cầu
Đầu tiên, bất đẳng thức có tính chất bắc cầu. Cụ thể, nếu ta có cùng lúc 2 biểu thức A < B và B < C thì các em có thể suy ra được A < C.
Tính chất cộng 2 vế của bất đẳng thức với 1 số
Tính chất cộng 2 vế của bất đẳng thức với 1 số khá đơn giản. Các em chỉ cần nhớ như sau:
A < B ⇔ A + C < B + C.
Tính chất cộng 2 bất đẳng thức cùng chiều
Nếu dữ kiện cho 2 bất đẳng thức cùng chiều A < C và B < D, các em sẽ kết luận được A + C < B + D.
Tính chất nhân 2 vế của bất đẳng thức với 1 số
Nếu đề bài cho A < B và C > 0 thì ta sẽ được AC < BC. Trong trường hợp A < B và C < 0, thì ta thu được AC > BC.
Tính chất nhân 2 bất đẳng thức cùng chiều
Nếu dữ kiện cung cấp 0 < A < B và 0 < C < D thì tính chất nhân 2 bất đẳng thức cùng chiều ta sẽ thu được kết quả AC < BD.
>> Tham khảo: Taxi đi từ nội bài về hà nội giá rẻ

Được ứng dụng vào nhiều lĩnh vực
Bất đẳng thức Cauchy-Schwarz (Cosi) là một công cụ toán học quan trọng và có rất nhiều ứng dụng trong các lĩnh vực khác nhau của toán học và các ngành khoa học. Dưới đây là một số ứng dụng chính của bất đẳng thức Cauchy-Schwarz:
Đại số tuyến tính và hình học
Bất đẳng thức tam giác: Bất đẳng thức Cauchy-Schwarz giúp chứng minh bất đẳng thức tam giác trong không gian vector. Điều này làm cơ sở cho nhiều bổ đề và định lý quan trọng trong hình học và đại số tuyến tính.
Giải tích và tích phân
Định lý Bô-lơ-ka - Khintchin: Bất đẳng thức Cauchy-Schwarz là công cụ chính để chứng minh định lý Bô-lơ-ka - Khintchin trong lý thuyết xác suất và phân phối.
Bất đẳng thức Jensen: Sử dụng để chứng minh bất đẳng thức Jensen trong lý thuyết xác suất và thống kê.
Lý thuyết hàm
Bất đẳng thức của Hardy: Bất đẳng thức Cauchy-Schwarz dẫn đến bất đẳng thức của Hardy, một bổ đề quan trọng trong phân tích hàm và lý thuyết bất đẳng thức.
Hình học
Bất đẳng thức Minkowski: Đây là một ứng dụng của bất đẳng thức Cauchy-Schwarz trong không gian hình học và lý thuyết ma trận.
Kỹ thuật chứng minh
Công cụ trong chứng minh các bất đẳng thức khác: Bất đẳng thức Cauchy-Schwarz thường được sử dụng như một công cụ quan trọng trong chứng minh các bất đẳng thức khác, bao gồm cả bất đẳng thức Bunyakovsky, bất đẳng thức Holder và nhiều bất đẳng thức khác trong toán học.
Lý thuyết hệ số tương quan
Bất đẳng thức về hệ số tương quan: Trong thống kê và xác suất, bất đẳng thức Cauchy-Schwarz được áp dụng để giới hạn các hệ số tương quan giữa các biến ngẫu nhiên.
Ứng dụng trong tính toán và kỹ thuật
Phân tích dữ liệu và xử lý tín hiệu: Bất đẳng thức Cauchy-Schwarz cũng có thể được sử dụng để phân tích dữ liệu và xử lý tín hiệu trong các ứng dụng kỹ thuật và công nghệ.
Tóm lại, bất đẳng thức Cauchy-Schwarz là một công cụ toán học quan trọng có rất nhiều ứng dụng rộng rãi trong lý thuyết và thực tiễn, từ các vấn đề đơn giản trong hình học đến những ứng dụng phức tạp trong lý thuyết xác suất, phân tích hàm và thống kê.
>> Tham khảo: Tạo dáng chụp ảnh trước gương nam