Công thức tính diện tích hình chữ nhật
Hình chữ nhật là một trong những hình học cơ bản trong toán học và đại số, được sử dụng rộng rãi trong cuộc sống hàng ngày, kiến trúc, và nhiều lĩnh vực khác. Dưới đây là lý thuyết cơ bản về hình chữ nhật:
Đặc điểm cơ bản của hình chữ nhật:
Định nghĩa: Hình chữ nhật là một loại tứ giác có cả bốn góc là góc vuông (90 độ) và các cạnh đối diện bằng nhau.
Tính đối xứng và tổng quát: Hình chữ nhật có tính đối xứng, điều này có nghĩa là diện tích và chu vi không thay đổi dù cho các cạnh có thể thay đổi vị trí.
Ứng dụng của hình chữ nhật:
Trong kiến trúc và xây dựng: Hình chữ nhật được sử dụng để biểu diễn các khuôn viên, mặt bằng công trình, phòng chứa, sàn nhà và các thành phần cấu trúc khác.
Trong thiết kế nội thất: Hình chữ nhật thường xuất hiện trong thiết kế và bố trí nội thất, như bàn làm việc, kệ sách, tủ quần áo và các vật dụng gia đình khác.
Trong giáo dục: Là một ví dụ trong giáo dục về hình học cơ bản, giúp học sinh hiểu về tính chất và tính toán với các hình học đơn giản.
Trong quản lý đất đai và kế hoạch đô thị: Diện tích của các khu đất, khu vực xây dựng và kế hoạch quy hoạch đô thị thường được tính toán dựa trên hình chữ nhật.
>> Xem thêm: Bất đẳng thức cosi

Học sinh trong giờ toán
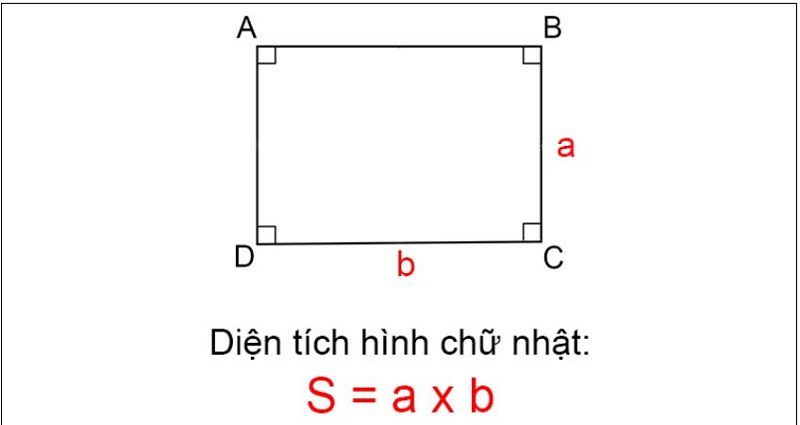
Diện tích
S của hình chữ nhật được tính bằng tích của hai cạnh gần nhau:
S = a x b
Trong đó:
S chính là diện tích của hình chữ nhật
a sẽ là chiều dài của hình chữ nhật
b sẽ là chiều rộng của hình chữ nhật
Ví dụ: Cho hình chữ nhật ABCD, biết chiều dài là 5cm và chiều rộng 3cm. Hãy sử dụng công thức tính diện tích hình chữ nhật để tính diện tích hình ABCD.
Áp dụng công thức ta có diện tích hình chữ nhật ABCD sẽ là:
5 x 3 = 15 cm2
Đáp số: 15 cm2
Diện tích hình chữ nhật
Khi tính diện tích của hình chữ nhật, có một số mẹo và lưu ý sau đây để giúp bạn thực hiện tính toán một cách chính xác và hiệu quả:
Xác định chiều dài và chiều rộng chính xác
Xác định rõ ràng: Đảm bảo rằng bạn đã xác định đúng chiều dài và chiều rộng của hình chữ nhật. Điều này đặc biệt quan trọng cho công thức tính diện tích hình chữ nhật nếu bạn có bản vẽ hoặc mô tả chi tiết của hình chữ nhật.
Sử dụng đúng đơn vị đo lường: Đảm bảo cả hai cạnh
a (chiều dài) và
b (chiều rộng) được đo bằng cùng một đơn vị, chẳng hạn như mét, centimet.
Sử dụng công thức diện tích đơn giản
Công thức tính diện tích: Sử dụng công thức
S= a x b
a là chiều dài và
b là chiều rộng của hình chữ nhật.
Tính toán dễ dàng hơn với các số nguyên: Nếu có thể, lựa chọn các giá trị nguyên cho chiều dài và chiều rộng sẽ giúp tính toán diện tích dễ dàng hơn.

Giờ học Toán trên lớpKiểm tra lại kết quả tính toán
Kiểm tra tính logic và hợp lý của kết quả: Sau khi tính toán xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác và hợp lý. Ví dụ, diện tích không thể âm và nên có giá trị dương.
Đối chiếu với mục đích sử dụng
Xác định mục đích sử dụng kết quả: Đối với các bài toán thực tế như thiết kế, xây dựng, quy hoạch đô thị, đảm bảo rằng kết quả tính toán được sử dụng một cách hợp lý và đáp ứng mục đích cụ thể của bài toán.
Sử dụng công cụ và phương tiện hỗ trợ
Sử dụng máy tính hoặc ứng dụng tính toán: Đối với các tính toán lớn hoặc cần sự chính xác cao, sử dụng máy tính hoặc các ứng dụng tính toán sẽ giúp bạn tiết kiệm thời gian và giảm thiểu sai sót.
>> Tham khảo: Xe từ sân bay nội bài về hải phòng