Diện tích tam giác vuông cân
Hình tam giác là hình học có 2 chiều phẳng với 3 đỉnh là 3 điểm không thẳng hàng. Đồng thời có 3 cạnh là 3 đoạn thẳng nối các đỉnh lại với nhau. Ngoài ra, tam giác còn được biết tới là hình đa giác với số cạnh ít nhất, đồng thời cũng là đa giác đơn và đa giác lồi với các góc có số đo luôn nhỏ hơn 180°.
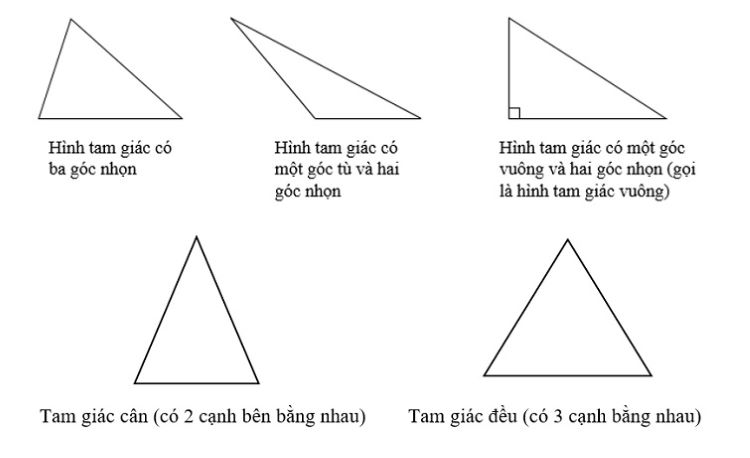
Các dạng hình tam giác
Trong toán học hiện nay, hình tam giác được chia ra thành nhiều loại khác nhau. Cụ thể phân loại như sau:
- Độ dài các cạnh gồm: tam giác thường, tam giác cân và tam giác đều.
- Số đo các góc trong gồm: tam giác vuông, tam giác tù, tam giác vuông cân và tam giác nhọn.
- Tính chất hình tam giác như sau:
- Tổng các góc trong của 1 tam giác có tổng bằng 180°.
- Trong hình tam giác, cạnh đối diện với góc lớn hơn sẽ là cạnh lớn hơn và điều ngược lại.
- Trọng tâm của hình tam giác chính là điểm giao nhau của 3 đường trung tuyến.
- Tâm đường tròn nội tiếp của một hình tam giác chính là điểm giao nhau của 3 đường phân giác.
- Tâm đường tròn ngoại tiếp của một hình tam giác là điểm giao nhau của 3 đường trung trực.
- Tỷ lệ giữa độ dài của mỗi cạnh tam giác với sin của góc đối diện là bằng nhau.
- Đường phân giác trong tam giác của 1 góc sẽ chia cạnh đối diện thành 2 đoạn thẳng có tỉ lệ với 2 cạnh kề 2 đoạn thẳng đó.
- Hiệu độ dài của hai cạnh tam giác sẽ luôn nhỏ hơn độ dài của mỗi cạnh và nhỏ hơn tổng độ dài của hai cạnh.
- Trực tâm của hình tam giác là điểm giao nhau của 3 đường cao.
- Bình phương độ dài 1 cạnh tam giác sẽ bằng tổng bình phương độ dài 2 cạnh còn lại trừ đi 2 lần tích giữa độ dài 2 cạnh đó với cosin của góc nằm xen giữa 2 cạnh đó.
- Đường trung bình của hình tam giác chính là đoạn thẳng nối trung điểm 2 cạnh tam giác.
Trước khi tìm hiểu về Diện tích tam giác vuông cân, ta cần hiểu tam giác vuông cân là gì? Tam giác vuông cân là một tam giác có 1 góc vuông và 2 góc còn lại có số đo bằng nhau, đồng thời 2 cạnh góc vuông có độ dài bằng nhau.
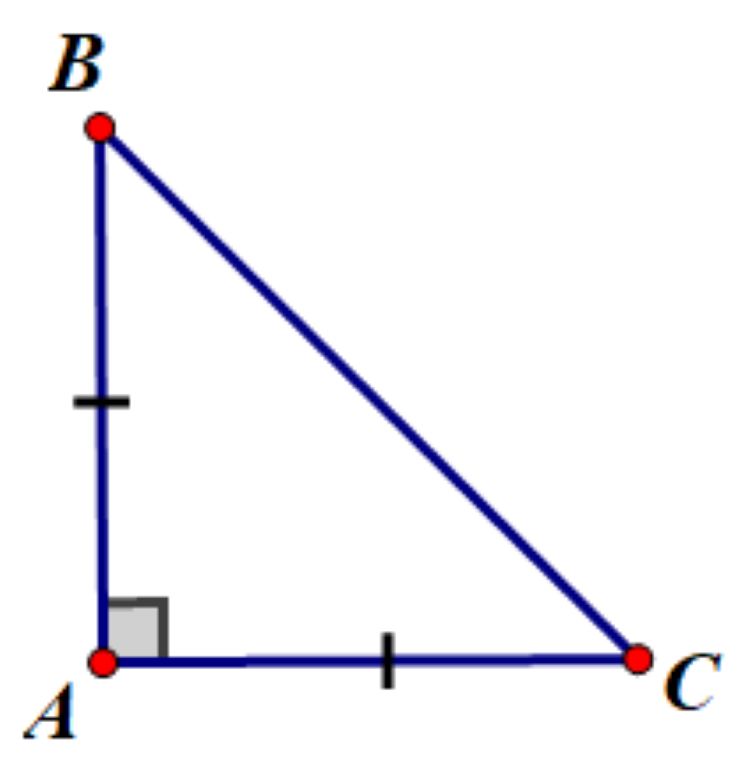
Tam giác vuông cân có 2 cạnh bằng nhau
Mỗi hình tam giác sẽ có cách tích diện tích khác nhau, dễ áp dụng hơn. Dưới đây là công thức và ví dụ cụ thể để các em tham khảo:
3.1. Công tính tính diện tích tam giác thường
Khái niệm: Tam giác thường là hình tam giác sở hữu độ dài các cạnh khác nhau, đồng thời số đo các góc cũng không giống nhau.
Công thức: Diện tích hình tam giác thường tính theo công thức: ½ tích của chiều cao hạ từ đỉnh xuống nhân với độ dài cạnh đối diện với đỉnh đó.
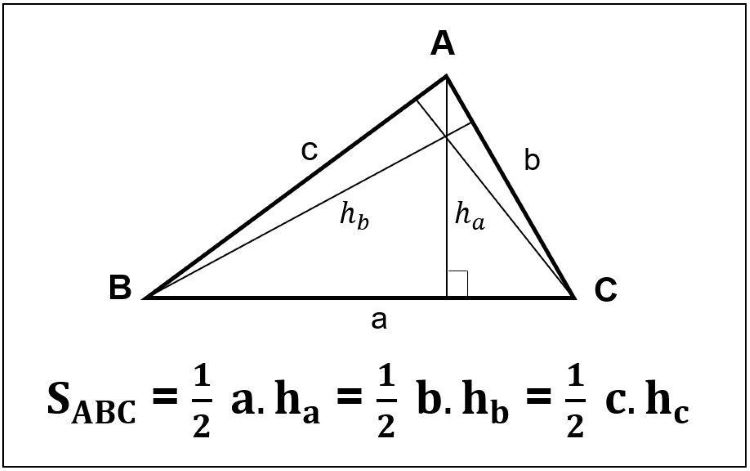
Công thức tính diện tích tam giác
Công thức như sau: S = (a x h)/2.
Trong đó:
a: Độ dài một cạnh của tam giác thường, h là chiều cao tương ứng của cạnh đó
Ví dụ: Một tam giác có độ dài cạnh đáy là 5cm với chiều cao là 2cm. Áp dụng công thức trên ta có: S=(5 x 2)/2 = 5 cm2.
3.2. Công thức tính diện tích cân
Khái niệm: Tam giác cân là hình tam giác với 2 cạnh bên bằng nhau.
Công thức: Diện tích hình tam giác cân bằng tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó đem chia cho 2.
Công thức như sau: S = (a x h)/2.
Trong đó: a: độ dài cạnh đáy của tam giác cân, còn h là chiều cao tương ứng của cạnh đáy đó
Ví dụ: Một tam giác cân có độ dài cạnh đáy là 5cm với chiều cao tương ứng là 4cm. Áp dụng công thức ta có: S= (5 x 4)/2 = 10 cm2.
3.3. Công thức tính diện tích tam giác đều
Định nghĩa: Tam giác đều là loại tam giác sở hữu 3 cạnh bằng nhau. Đồng thời có các góc bằng nhau và bằng 60 độ.
Công thức: Diện tích tam giác đều được tính bằng tích của chiều cao nhân với độ dài cạnh đó, sau đó đem chia với 2.
Công thức tính diện tích tam giác đều
Công thức như sau: S = (a x h)/2.
Trong đó: a: độ dài một cạnh của tam giác đều, h là độ dài chiều cao tương ứng của cạnh đó
Ví dụ: Cho Một tam giác đều có độ dài cạnh đáy là 6cm với chiều cao là 5cm. Áp dụng công thức trên ta có: S= (6 x 5)/2 = 15 cm2.
3.4. Công thức tính Diện tích tam giác vuông
Định nghĩa: Tam giác vuông là hình tam giác sở hữu một góc vuông 90°.
Công thức: Diện tích hình tam giác vuông cân sẽ được tính bằng ½ tích của chiều cao với chiều dài cạnh đáy. Tuy nhiên, do loại tam giác này có 2 cạnh góc vuông nên chiều cao sẽ ứng với 1 cạnh góc vuông, còn chiều dài cạnh đáy sẽ ứng với cạnh góc vuông còn lại.
Công thức như sau: S = (a x h)/2.
Trong đó: a là độ dài một cạnh góc vuông. còn h là độ dài cạnh góc vuông còn lại.
Ví dụ: Một tam giác vuông có hai cạnh góc vuông lần lượt là 9cm và 6cm.
Áp dụng công thức tính ta có S là: (9 x 6)/2 = 27 cm2.
3.5. Công thức tính Diện tích tam giác vuông cân
Định nghĩa: Tam giác vuông cân là hình tam giác vừa vuông (có góc vuông bằng 90 độ) vừa cân tại đỉnh góc vuông.
Công thức Diện tích tam giác vuông cân: S = ½ x a2.
Trong đó: a là độ dài một cạnh góc vuông của tam giác vuông cân.
Ví dụ: Cho tam giác vuông cân ABC tại A, có độ dài AB = AC = 10cm. Áp dụng công thức trên ta có, S= ½ x 102 = 50cm2.
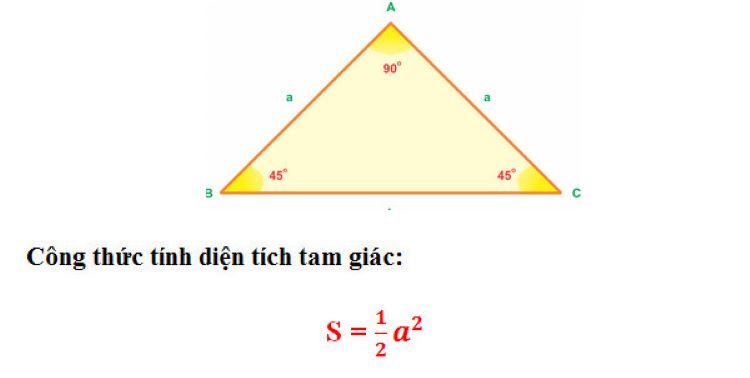
Công thức tính diện tích tam giác vuông cânKhông phải bài toán tính diện tích tam giác nào nào cũng có sẵn các thông số tương ứng với công thức chung. Khi đó, dưới đây là một số dạng tính diện tích tam giác:
1. Tính diện tích hình tam giác khi biết cạnh đáy và chiều cao
Với bài toán tính S tam giác cho biết cạnh đáy và chiều cao, bạn có thể áp dụng công thức tích một nửa chiều cao nhân với cạnh đáy tương ứng chiếu lên.
2. Tính diện tích hình tam giác khi biết chiều dài các cạnh
Với bài toán cho biết chiều dài các cạnh, bạn có thể tính diện tích hình tam giác theo hướng dẫn sau đây:
Bước 1: Tính nửa chu vi của hình tam giác bằng cách cộng chiều dài 3 cạnh với nhau rồi đem nhân với ½.
Bước 2: Áp dụng công thức Heron để tính diện tích theo nửa chu vi và chiều dài các cạnh với công thức sau: S = √p x (p – a) x (p – b) x ( p – c).
3. Tính diện tích hình tam giác đều khi biết một cạnh của tam giác
Về tính chất, tam giác đều có 3 cạnh và 3 góc bằng nhau. Do đó, bài toán cho biết chiều dài của cạnh suy ra đây là chiều dài của cả 3 cạnh. Sau đó, bạn hãy sử dụng công thức tính diện tích bằng (bình phương của chiều dài 1 cạnh tam giác đều) nhân với (căn bậc 3 chia 4).
4. Tính diện tích áp dụng hàm lượng giác
Với bài toán cho biết hai cạnh kề nhau và góc tạo bởi chúng. Bạn có thể áp dụng công thức tính dựa theo hàm công thức lượng giác để tính diện tích hình tam giác sau đây:
Diện tích = (Tích hai cạnh kề của tam giác chia 2) đem nhân với số sin góc nằm giữa 2 cạnh đó.
5. Tính diện tích tam giác khi biết chu vi và bán kính đường tròn nội tiếp
Khi đã biết chu vi và bán kính đường tròn nội tiếp, bạn có thể tìm ra diện tích hình tam giác bằng cách: Lấy nửa chu vi tam giác đem nhân với bán kính đường tròn nội tiếp.