Bất đẳng thức cosi
1.1. Bất đẳng thức Cô – si cho 2 số, 3 số
Cho hai số không âm a, b, ta luôn có đẳng thức sau:
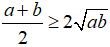
Dấu “=” đẳng thức xảy ra khi và chỉ khi giá trị a=b.
Mở rộng:
a. Với các số a, b, c không âm, ta luôn có:
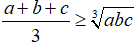
Dấu “=” đẳng thức xảy ra khi và chỉ khi a=b=c.
b. Với n số ai, i=1,n không âm, ta cũng luôn có:
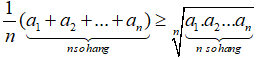
Dấu “=” đẳng thức xảy ra khi và chỉ khi giá trị a1=a2=...=an
1.2. Bất đẳng thức Bunhiacopxki
Cho a1, a2, b1, b2 là những số thực, ta luôn có:
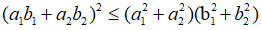
Dấu đẳng thức xảy ra khi
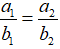
Mở rộng: Với các số thực a1, a2, b1, b2, a3, b3, ta cũng luôn có:
Dấu đẳng thức xảy ra khi và chỉ khi:
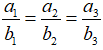
>> Xem thêm: Công thức tính diện tích hình chữ nhật
Câu 1: Cho a,b>0. Chứng minh rằng:
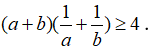
Lời giải:
Áp dụng bất đẳng thức Cô-si:
Cho cặp số a, b, ta có được:
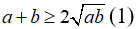
Cho cặp số Chứng minh theo bất đẳng thức bằng Cô-si, Bunhiacopxki, ta có được:
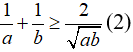
Nhân hai vế tương ứng của (1), (2), ta được như sau:
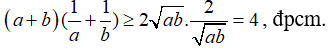
Dấu “=” xảy ra khi và chỉ khi:
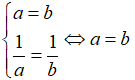
Câu 2: Cho ba số dương a, b, c. Chứng minh rằng:
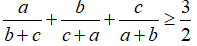
Giải.
Ta có biểu thức sau
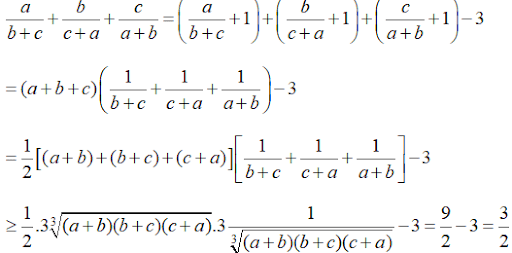
Dấu đẳng thức xảy ra khi:
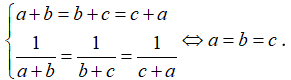
Câu 3: Chứng minh rằng với a, b, c tùy ý ta luôn có đẳng thức:
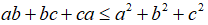
Lời giải:
Theo bài ra, ta có:
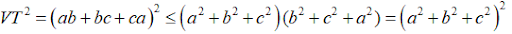
Lấy căn bậc hai của hai vế, ta sẽ có được :
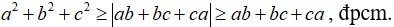
>> Tham khảo: Taxi 7 chỗ đi nội bài giá rẻ
Bất đẳng thức Cauchy, hay còn gọi là bất đẳng thức Cauchy. Đây là một công cụ toán học mạnh mẽ được sử dụng rộng rãi để giải quyết nhiều dạng bài toán khác nhau. Đặc biệt đối với dạng bài tìm giá trị nhỏ nhất và lớn nhất của các hàm số. Dưới đây là một số ví dụ điển hình về ứng dụng của Bất đẳng thức cauchy:
Giải phương trình và hệ phương trình: Với Đẳng thức Cosi có thể được áp dụng để đơn giản hóa và giải các phương trình hay hệ phương trình bằng cách thiết lập mối liên hệ giữa các biến số với nhau. Từ đó đưa ra các điều kiện cho nghiệm.
Chứng minh các bất đẳng thức: Trong một số trường hợp, bất đẳng thức Cauchy được sử dụng để chứng minh một số bất đẳng thức khác nhau. Ví dụ, ta có thể apd dụng nó để chứng minh rằng tổng bình phương của các biến lớn hơn hay bằng tích của chúng.
Tìm được giá trị lớn nhất và nhỏ nhất của các biểu thức: Bất đẳng thức này cũng rất có ích trong việc tìm giá trị lớn nhất và nhỏ nhất của các biểu thức. Nhất là trong các bài toán liên quan đến các hàm số và các biến số.
Ứng dụng của bất đẳng thức cachy
Bất đẳng thức là một dạng bài tập được đánh giá là khó và là câu để phân loại học sinh. Tuy nhiên nếu cứ suy nghĩ mặc định, đây là dạng bài khó, chỉ chiếm 1 phần điểm rất nhỏ, nên thôi bỏ qua thì cũng là suy nghĩ chưa đúng đắn.
Do đó, để làm tốt dạng bài này, việc đầu tiên là loại bỏ suy nghĩ: dạng khó này thôi bỏ qua không học. Phải luôn nhắc nhở bạn thân chẳng có dạng bài nào khó, nếu chưa bắt tay vào làm.
Bên cạnh đó, để nhớ rõ kiến thức cần tập trung đọc cái tài liệu, tìm hiểu các kiến thức nền tảng nhất. Chớ vội xem đến các bài khó, hãy bắt đầu từ các dạng bài dễ, cơ bản nhất. Điều này giúp cho bạn có sự thích thú và không quá khó khăn trong quá trình tìm hiểu.
Hơn nữa, để tăng hiệu quả và duy trì trong thời gian lâu dài, hãy làm việc này cùng với bạn bè, thầy cô. Những thắc mắc của bạn trong quá trình trao đổi sẽ dần được gợi mở và hiểu bài.
Việc học không bao giờ là chuyện dễ dàng. Nhưng bằng sự bền bỉ, chắc chắn nỗ lực của bạn sẽ được đền đáp. Và tự học là phương pháp hiệu quả để học. Không ngừng tìm tòi và nghiên cứu kiến thức không chỉ giúp bạn hiểu kiến thức mà còn nhớ lâu kiến thức hiệu quả.
Ngoài ra, khi làm bài cần chú ý, đối với dạng bài chứng minh dựa vào bất đẳng thức cauchy hay các bài toán chứng minh. Cần lưu ý , trong khi làm không được quên điều kiện dấu “=” xảy ra của bất đẳng thức. Nếu có thể, hãy tìm thêm một phương pháp khác đi kèm hoặc chứng minh lại.
Lời kết:
Tóm lại, bất đẳng thức Cosi là một công cụ lý thuyết, một phương pháp thiết thực cần nhớ để giải quyết và chứng minh nhiều vấn đề toán học phức tạp. Sự hiểu biết và áp dụng thành thạo bất đẳng thức này giúp chúng ta nâng cao khả năng giải toán và phân tích toán học.