Đường trung tuyến là gì?
Khái niệm đường trung tuyến
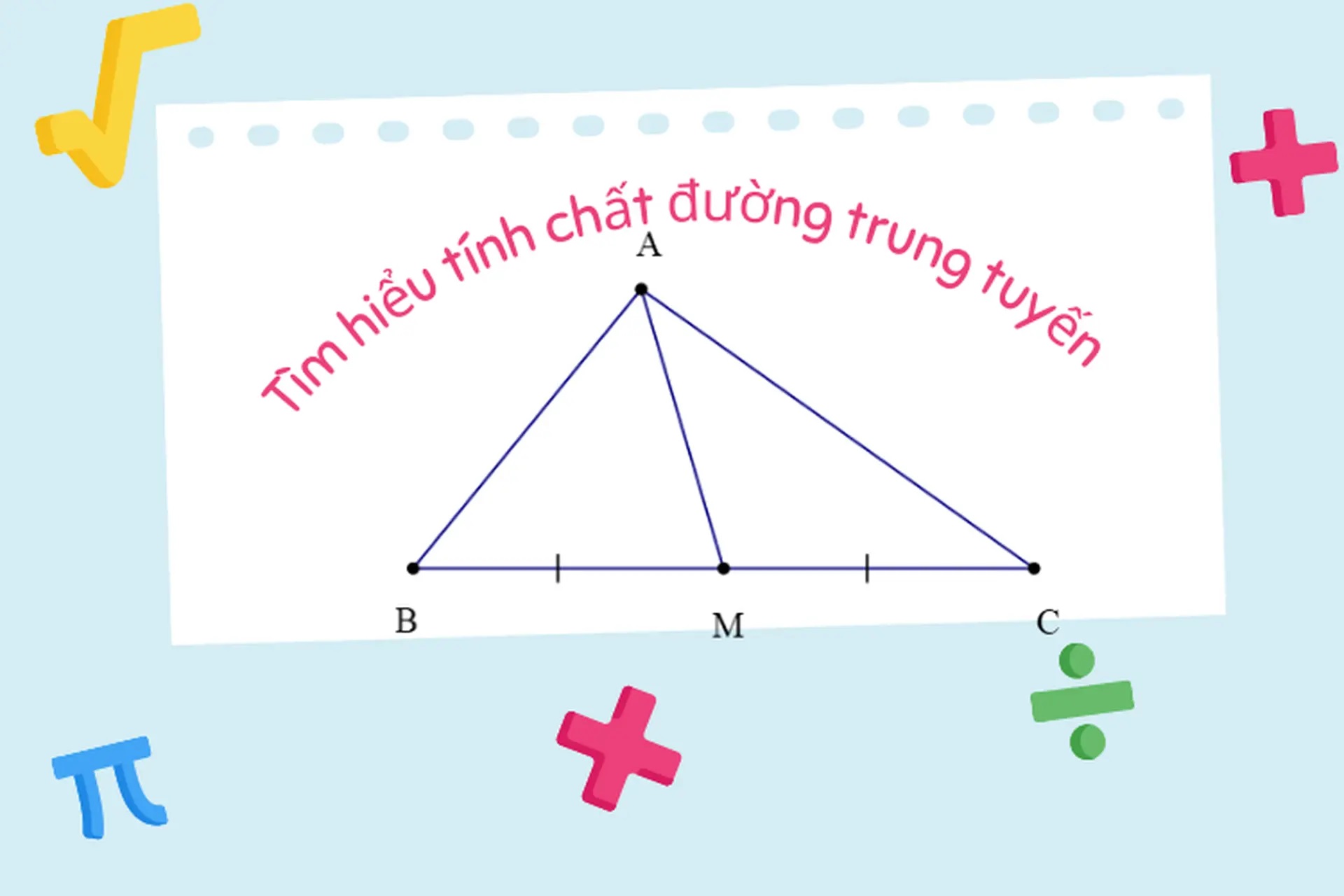
Đường trung tuyến của một tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện.
Nói đơn giản, nếu bạn tìm được trung điểm của một cạnh trong tam giác, sau đó nối trung điểm đó với đỉnh đối diện thì đoạn thẳng vừa nối chính là đường trung tuyến.
Định nghĩa chuẩn
Trong tam giác, đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đối diện được gọi là đường trung tuyến của tam giác.
Đường trung tuyến trong tam giác
Số lượng đường trung tuyến
Mỗi tam giác có ba đường trung tuyến, tương ứng với ba đỉnh của tam giác.
Ví dụ trong tam giác ABC:
M là trung điểm của cạnh BC thì AM là đường trung tuyến
N là trung điểm của cạnh AC thì BN là đường trung tuyến
P là trung điểm của cạnh AB thì CP là đường trung tuyến
Tính chất của đường trung tuyến
Ba đường trung tuyến đồng quy
Một tính chất rất quan trọng của đường trung tuyến là:
Ba đường trung tuyến của một tam giác luôn cắt nhau tại một điểm duy nhất.
Điểm đó được gọi là trọng tâm của tam giác.
Tính chất về tỉ lệ đoạn thẳng
Giả sử:
Tam giác ABC
M là trung điểm của BC
AM là đường trung tuyến
G là trọng tâm tam giác
Khi đó, trọng tâm G chia đường trung tuyến AM theo tỉ lệ:
AG : GM=2 : 1
Viết dưới dạng công thức:
AG=(2/3) x AM
GM=(1/3) x AM
 Tìm hiểu về đường trung tuyến
Tìm hiểu về đường trung tuyếnĐể vẽ đường trung tuyến của một tam giác, bạn làm theo các bước sau:
Bước xác định trung điểm của cạnh
Chọn một cạnh của tam giác làm cạnh đối diện với đỉnh cần vẽ trung tuyến.
Xác định trung điểm của cạnh đó.
Ví dụ:
Trong tam giác ABC, muốn vẽ đường trung tuyến từ đỉnh A thì cần xác định trung điểm M của cạnh BC.
M là trung điểm của BC khi:
BM=MC
Bước nối trung điểm với đỉnh đối diện
Dùng thước kẻ nối đỉnh A với trung điểm M của cạnh BC.
Đoạn thẳng AM vừa vẽ chính là đường trung tuyến của tam giác ABC.
Kiểm tra lại đường trung tuyến
Đường trung tuyến phải thỏa mãn đầy đủ các điều kiện sau:
Đi qua một đỉnh của tam giác
Đi qua trung điểm của cạnh đối diện
Không bắt buộc phải vuông góc với cạnh đáy
Nếu thỏa mãn đủ ba điều kiện trên thì bạn đã vẽ đúng đường trung tuyến.
 Đường trung tuyến
Đường trung tuyếnDưới đây là những dạng bài tập phổ biến nhất về đường trung tuyến trong chương trình Toán THCS, đặc biệt lớp 7. Mỗi dạng đều kèm hướng làm ngắn gọn để bạn áp dụng ngay.
Dạng nhận biết đường trung tuyến
Đặc điểm bài toán
Bài toán cho sẵn hình vẽ hoặc dữ kiện và yêu cầu xác định một đoạn thẳng có phải là đường trung tuyến hay không.
Cách làm
Xác định đoạn thẳng đó có:
Nối từ một đỉnh của tam giác
Đi qua trung điểm của cạnh đối diện
Nếu thỏa mãn hai điều kiện trên thì đó là đường trung tuyến.
Dạng chứng minh một đoạn thẳng là đường trung tuyến
Đặc điểm bài toán
Yêu cầu chứng minh đoạn thẳng nối từ một đỉnh đến một điểm nào đó là đường trung tuyến.
Cách làm
Thực hiện theo hai bước:
Chứng minh điểm đó là trung điểm của cạnh đối diện
Kết luận đoạn thẳng nối từ đỉnh đến trung điểm là đường trung tuyến
Dạng bài liên quan đến trọng tâm tam giác
Đặc điểm bài toán
Bài toán cho tam giác có các đường trung tuyến và trọng tâm, yêu cầu xác định vị trí hoặc tính độ dài các đoạn thẳng.
Kiến thức cần nhớ
Ba đường trung tuyến cắt nhau tại trọng tâm
Trọng tâm chia mỗi đường trung tuyến theo tỉ lệ 2 : 1
Công thức thường dùng
AG=(2/3) x AM
GM=(1/3) x AM
Dạng bài tính độ dài đoạn thẳng trên đường trung tuyến
Đặc điểm bài toán
Cho độ dài đường trung tuyến hoặc một đoạn trên trung tuyến, yêu cầu tính đoạn còn lại.
Hướng làm
Áp dụng tỉ lệ của trọng tâm:
AG : GM=2 : 1
Hoặc sử dụng công thức:
AM=3/2 x AG
AM=3 x GM
Dạng bài chứng minh các đoạn thẳng bằng nhau
Đặc điểm bài toán
Yêu cầu chứng minh các đoạn thẳng liên quan đến trung tuyến bằng nhau.
Hướng làm
Chứng minh điểm là trung điểm
Sử dụng tính chất trung điểm chia đoạn thẳng thành hai phần bằng nhau
Kết hợp tính chất của trọng tâm nếu có
Dạng bài kết hợp đường trung tuyến với các đường đặc biệt khác
Đặc điểm bài toán
Bài toán có đường trung tuyến kết hợp với:
Đường cao
Đường trung trực
Đường phân giác
Cách làm
Phân biệt rõ từng loại đường dựa vào:
Vị trí đi qua
Điều kiện vuông góc
Điều kiện chia góc hoặc chia cạnh

Công thức tính độ dài đường trung tuyến
Ví dụ 1
Cho tam giác ABC
M là trung điểm của BC
Chứng minh AM là đường trung tuyến của tam giác ABC
Giải:
Vì M là trung điểm của BC nên BM=MC
AM nối từ đỉnh A đến trung điểm M
Suy ra AM là đường trung tuyến
Ví dụ 2
Cho tam giác ABC
AM là đường trung tuyến
G là trọng tâm
Biết AM=9 cm
Tính AG
Áp dụng công thức:
AG=(2/3) x AM
AG=(2/3) x 9
AG=6 cm
Nhầm trung điểm với điểm bất kỳ trên cạnh
Nhầm đường trung tuyến với đường trung trực
Quên tỉ lệ AG : GM=2 : 1
Vẽ sai vị trí trung điểm
Mẹo ghi nhớ đường trung tuyến
Trung tuyến luôn đi qua đỉnh
Trung tuyến luôn đi qua trung điểm cạnh đối diện
Ba trung tuyến cắt nhau tại trọng tâm
Trọng tâm chia trung tuyến theo tỉ lệ 2 : 1
Qua bài viết này, bạn đã hiểu rõ đường trung tuyến là gì, các tính chất quan trọng, công thức liên quan và cách áp dụng vào bài tập. Đây là kiến thức nền tảng trong hình học tam giác, xuất hiện rất nhiều trong kiểm tra và thi cử. Việc nắm chắc đường trung tuyến sẽ giúp học sinh học tốt các phần kiến thức hình học nâng cao sau này.