Bất đẳng thức cosi
Trong chương trình Toán học từ THCS đến THPT, bất đẳng thức là một mảng kiến thức quan trọng, thường xuyên xuất hiện trong các bài kiểm tra, bài thi học sinh giỏi và cả đề thi tuyển sinh. Trong số các bất đẳng thức quen thuộc, bất đẳng thức được xem là công cụ nền tảng, dễ nhớ nhưng lại có khả năng ứng dụng rất linh hoạt. Việc nắm vững bất đẳng thức Cosi không chỉ giúp học sinh giải nhanh các bài toán tìm giá trị lớn nhất – nhỏ nhất mà còn hỗ trợ tốt trong chứng minh bất đẳng thức phức tạp. Bài viết dưới đây sẽ giúp bạn hiểu rõ bản chất, cách sử dụng và những lưu ý quan trọng khi áp dụng bất đẳng thức Cauchy .
Bất đẳng thức Cauchy là một bất đẳng thức cơ bản trong Toán học, dùng để so sánh mối quan hệ giữa tổng và tích của các số không âm. Đây là dạng bất đẳng thức thường được giới thiệu sớm cho học sinh vì có công thức đơn giản, dễ ghi nhớ và mang tính trực quan cao. Trong nhiều tài liệu, bất đẳng thức Cauchy còn được gọi là bất đẳng thức trung bình cộng – trung bình nhân.
Bản chất của bất đẳng thức Cauchy cho thấy rằng với các số không âm, trung bình cộng luôn lớn hơn hoặc bằng trung bình nhân. Điều này phản ánh quy luật tự nhiên và giúp học sinh hiểu sâu hơn về sự phân bố của các giá trị số.
Với hai số không âm a và b, bất đẳng thức Cauchy có dạng:
Trung bình cộng của a và b luôn lớn hơn hoặc bằng căn bậc hai của tích a và b.
Với ba số không âm a, b, c, bất đẳng thức Cauchy được mở rộng theo dạng trung bình cộng của ba số luôn lớn hơn hoặc bằng căn bậc ba của tích ba số đó.
Với n số không âm, bất đẳng thức Cauchy vẫn được giữ nguyên bản chất và có thể áp dụng cho nhiều bài toán nâng cao.
 Bất đẳng thức
Bất đẳng thứcĐiều kiện xảy ra dấu bằng
Một điểm rất quan trọng khi sử dụng bất đẳng thức Cauchy là điều kiện xảy ra dấu bằng. Dấu bằng xảy ra khi và chỉ khi các số bằng nhau. Đây là chìa khóa giúp học sinh tìm ra giá trị lớn nhất hoặc nhỏ nhất của biểu thức trong các bài toán cực trị. Nếu bỏ qua điều kiện này, lời giải rất dễ bị thiếu hoặc sai kết luận.
Bất đẳng thức Cauchy cho hai số
Đây là dạng đơn giản nhất và cũng là dạng được sử dụng nhiều nhất trong chương trình THCS. Các bài toán thường yêu cầu so sánh tổng và tích của hai số dương hoặc chứng minh một biểu thức luôn không nhỏ hơn một giá trị cho trước. Dạng này giúp học sinh làm quen với tư duy bất đẳng thức và rèn luyện khả năng biến đổi biểu thức.
Bất đẳng thức Cauchy cho ba số
Khi mở rộng sang ba số, học sinh cần chú ý đến tính đối xứng của biểu thức. Nhiều bài toán yêu cầu tìm giá trị nhỏ nhất của tổng khi biết tích không đổi, hoặc ngược lại. Việc áp dụng bất đẳng thức Cauchy cho ba số thường xuất hiện trong các đề thi học sinh giỏi cấp cơ sở.
Bất đẳng thức Cauchy cho nhiều số dương
Ở bậc THPT, đặc biệt trong các bài toán nâng cao, bất đẳng thức Cauchy được áp dụng cho nhiều số dương. Khi đó, học sinh cần linh hoạt trong việc nhóm các số và nhận biết cấu trúc phù hợp để áp dụng bất đẳng thức. Dạng này đòi hỏi tư duy tổng quát và khả năng biến đổi linh hoạt.
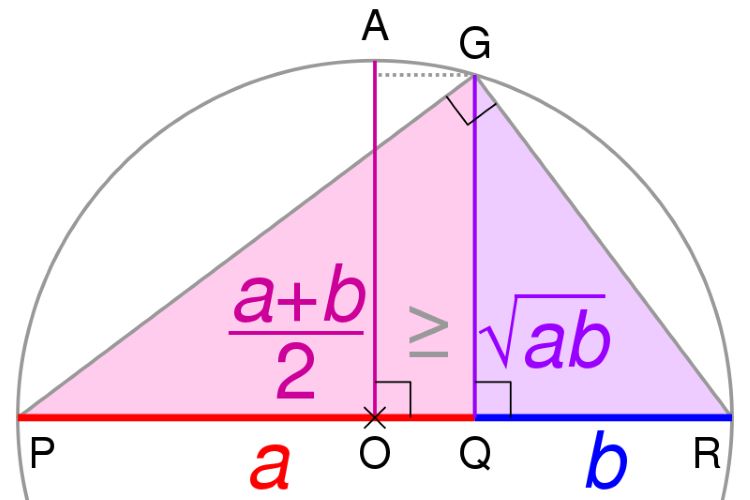 Chứng minh không cần lời
Chứng minh không cần lờiNhận biết bài toán có thể dùng bất đẳng thức Cauchy
Không phải bài toán bất đẳng thức nào cũng nên áp dụng Cosi. Những bài toán phù hợp thường có các dấu hiệu như xuất hiện tổng và tích của các số không âm, hoặc yêu cầu tìm giá trị lớn nhất, nhỏ nhất của biểu thức đối xứng. Việc nhận biết đúng dạng bài sẽ giúp học sinh tiết kiệm thời gian và tránh lan man trong quá trình giải.
Kỹ thuật tách ghép để áp dụng Cosi
Trong nhiều bài toán, biểu thức ban đầu không có dạng chuẩn để áp dụng bất đẳng thức . Khi đó, học sinh cần sử dụng kỹ thuật tách ghép số hạng để đưa biểu thức về dạng tổng của các số không âm. Đây là kỹ năng quan trọng và cần được luyện tập thường xuyên.
Kết hợp bất đẳng thức với các bất đẳng thức khác
Bất đẳng thức Cauchy thường không đứng riêng lẻ mà được kết hợp với các bất đẳng thức quen thuộc khác như Bunhiacopxki hoặc các bất đẳng thức cơ bản. Việc kết hợp đúng cách sẽ giúp bài toán trở nên ngắn gọn và chặt chẽ hơn.
Ví dụ cơ bản về bất đẳng thức cho hai số
Cho hai số không âm a và b. Chứng minh rằng tổng của a và b luôn lớn hơn hoặc bằng hai lần căn bậc hai của tích a và b.
Áp dụng bất đẳng thức cho hai số không âm, ta có trung bình cộng của a và b luôn lớn hơn hoặc bằng trung bình nhân của chúng. Từ đó suy ra tổng a cộng b không nhỏ hơn hai lần căn bậc hai của a nhân b.
Dấu bằng xảy ra khi và chỉ khi a bằng b. Ví dụ này giúp học sinh làm quen với dạng cơ bản nhất của bất đẳng thức và hiểu rõ vai trò của điều kiện xảy ra dấu bằng.
Ví dụ bất đẳng thức Cauchy cho ba số dương
Cho ba số dương a, b, c. Chứng minh rằng tổng a cộng b cộng c luôn lớn hơn hoặc bằng ba lần căn bậc ba của tích a nhân b nhân c.
Trong trường hợp này, bất đẳng thức được mở rộng cho ba số không âm. Ta sử dụng dạng trung bình cộng – trung bình nhân cho ba số để suy ra bất đẳng thức cần chứng minh.
Khi a, b và c bằng nhau thì dấu bằng xảy ra. Ví dụ này thường xuất hiện trong các bài toán tìm giá trị nhỏ nhất của tổng khi biết tích của ba số không đổi.
Ví dụ tìm giá trị nhỏ nhất bằng bất đẳng thức Cauchy
Cho hai số dương x và y thỏa mãn tích x nhân y bằng một hằng số không đổi. Tìm giá trị nhỏ nhất của biểu thức x cộng y.
Do x và y là các số dương nên có thể áp dụng bất đẳng thức Cauchy . Theo bất đẳng thức này, tổng x cộng y luôn lớn hơn hoặc bằng hai lần căn bậc hai của tích x nhân y. Vì tích đã cho là hằng số, nên giá trị nhỏ nhất của tổng đạt được khi x bằng y.
Ví dụ này cho thấy bất đẳng thức Cauchy là công cụ rất hiệu quả trong các bài toán cực trị.
Ví dụ nâng cao kết hợp bất đẳng thức Cauchy
Cho ba số dương a, b, c có tổng không đổi. Chứng minh rằng tích a nhân b nhân c đạt giá trị lớn nhất khi a, b, c bằng nhau.
Từ bất đẳng thức Cauchy cho ba số, ta có trung bình cộng của a, b, c luôn lớn hơn hoặc bằng căn bậc ba của tích a nhân b nhân c. Khi tổng đã cố định, trung bình cộng cũng cố định, do đó tích đạt giá trị lớn nhất khi dấu bằng xảy ra, tức là khi ba số bằng nhau.
Dạng bài này thường gặp trong các đề thi học sinh giỏi và giúp rèn luyện tư duy sử dụng bất đẳng thức Cauchy một cách linh hoạt.
 Học sinh ôn lại bài
Học sinh ôn lại bàiKhi nào nên dùng bất đẳng thức Cauchy
Bất đẳng thức Cauchy nên được sử dụng khi bài toán liên quan đến tổng và tích của các số không âm hoặc khi cần tìm giá trị lớn nhất, nhỏ nhất của biểu thức đối xứng.
Bất đẳng thức Cauchy khác gì so với AM-GM
Thực chất, bất đẳng thức Cauchy chính là một dạng của AM-GM. Tuy nhiên, trong chương trình phổ thông, tên gọi bất đẳng thức Cauchy thường được sử dụng để giúp học sinh dễ ghi nhớ và áp dụng.
Học sinh lớp mấy cần nắm vững bất đẳng thức Cauchy
Học sinh từ bậc THCS đã bắt đầu tiếp cận bất đẳng thức . Việc nắm vững kiến thức này sẽ giúp các em học tốt hơn ở bậc THPT và các kỳ thi quan trọng.
Bất đẳng thức là một trong những bất đẳng thức nền tảng và quan trọng nhất trong Toán học phổ thông. Việc hiểu rõ bản chất, công thức và cách áp dụng không chỉ giúp học sinh giải nhanh các bài toán mà còn rèn luyện tư duy logic và khả năng biến đổi linh hoạt. Nếu được luyện tập đúng cách, bất đẳng thức Cauchy sẽ trở thành công cụ đắc lực giúp học sinh chinh phục nhiều dạng bài khó trong các kỳ thi.