Đường trung tuyến là gì
Đường trung tuyến trong toán học là một đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện với đỉnh đó. Đường trung tuyến chia tam giác thành hai phần có diện tích bằng nhau. Đây là một yếu tố quan trọng trong hình học, đặc biệt trong việc nghiên cứu các tính chất và đặc điểm của tam giác.
Các điểm quan trọng liên quan đến đường trung tuyến:
- Trung điểm của cạnh đối diện: Đường trung tuyến luôn bắt đầu từ một đỉnh và kết thúc tại trung điểm của cạnh đối diện.
- Trọng tâm: Ba đường trung tuyến trong một tam giác luôn cắt nhau tại một điểm gọi là trọng tâm. Trọng tâm chia mỗi đường trung tuyến thành hai phần có tỉ lệ 2:1, trong đó phần gần đỉnh gấp đôi phần gần trung điểm.
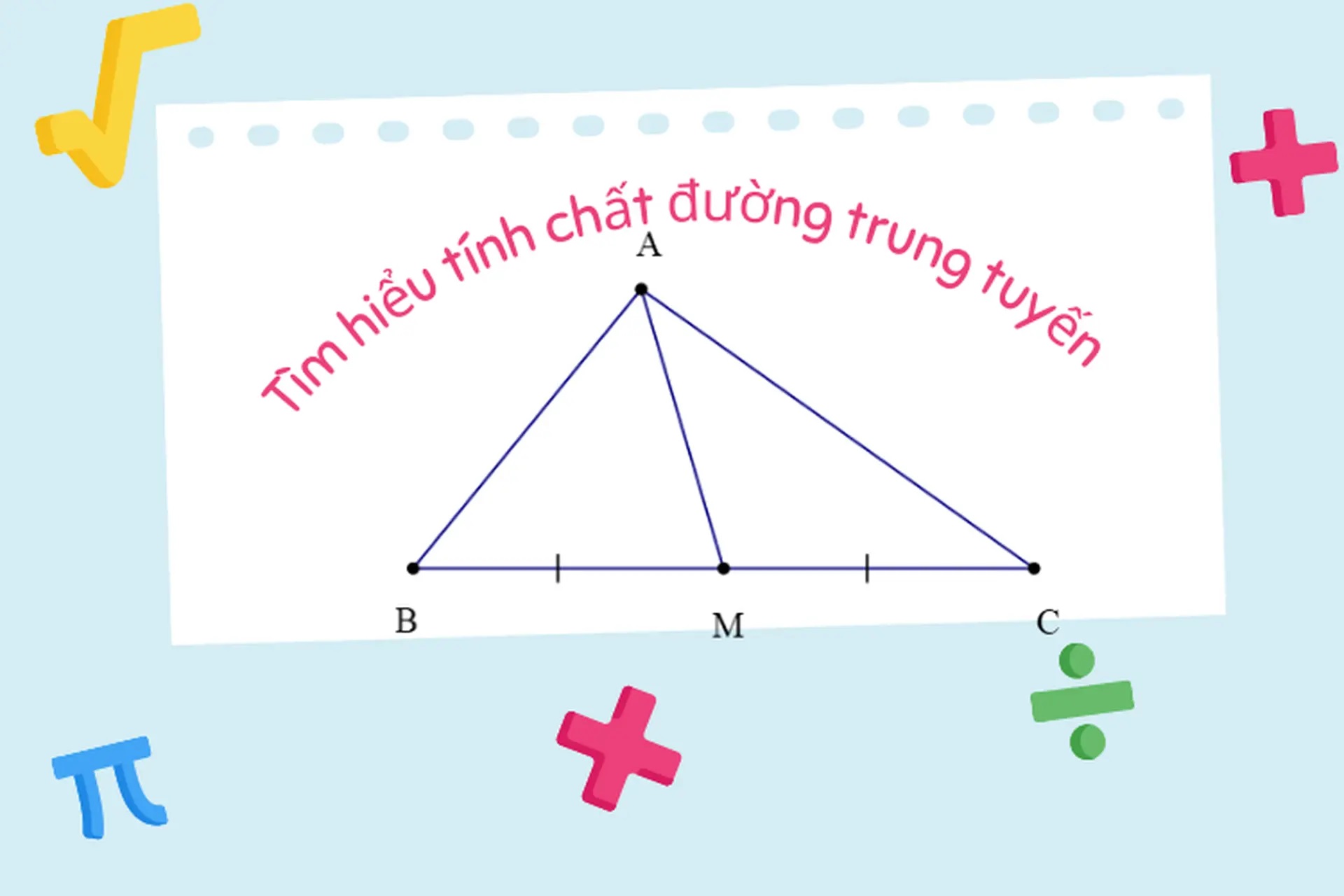
Tìm hiểu về đường trung tuyếnĐể tính độ dài của đường trung tuyến trong tam giác, chúng ta có thể sử dụng công thức đường trung tuyến dựa trên các cạnh của tam giác. Nếu tam giác có ba cạnh a, b, và c, thì độ dài của đường trung tuyến ứng với mỗi cạnh được tính theo công thức:
Công thức tính đường trung tuyến trong tam giác:
Giả sử tam giác có các cạnh a, b, c, và m_a, m_b, m_c lần lượt là các đường trung tuyến đối diện với các cạnh a, b, c.
Công thức tính độ dài của đường trung tuyến m_a đối diện với cạnh a:
mₐ = √((2b² + 2c² - a²) / 4)
Tương tự, các đường trung tuyến m_b và m_c đối diện với các cạnh b và c có công thức:
mb = √((2a² + 2c² - b²) / 4)
m𝑐 = √((2a² + 2b² - c²) / 4)
Ý nghĩa của các công thức:
m_a, m_b, m_c là độ dài của các đường trung tuyến đối diện với các cạnh a, b, và c của tam giác.
Công thức này sử dụng các cạnh của tam giác để tính độ dài của các đường trung tuyến mà không cần phải biết góc giữa các cạnh.
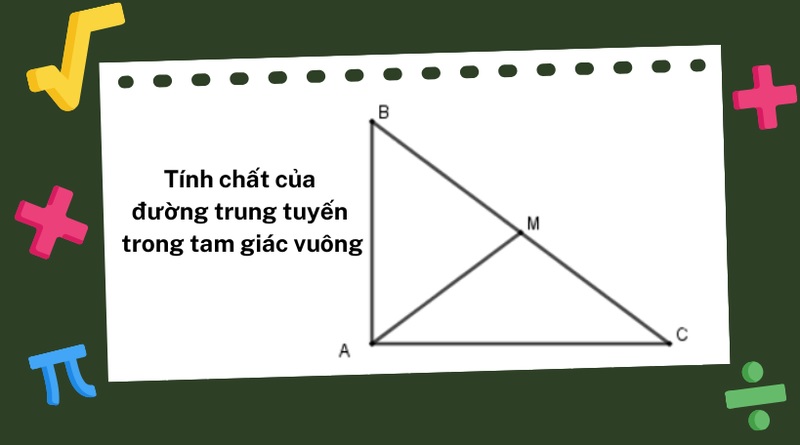
Tính chất của đường trung tuyến trong tam giác vuôngĐường trung tuyến là gì? Tính chất của đường trung tuyến trong tam giác bao gồm một số đặc điểm quan trọng sau:
- Đoạn thẳng nối từ đỉnh đến trung điểm của cạnh đối diện: Đường trung tuyến trong một tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Điều này có nghĩa là đường trung tuyến chia cạnh đối diện thành hai đoạn thẳng bằng nhau.
- Tính chất chia tam giác thành hai phần có diện tích bằng nhau: Đường trung tuyến chia tam giác thành hai phần có diện tích bằng nhau. Điều này có thể thấy rõ nếu bạn cắt tam giác dọc theo đường trung tuyến; mỗi phần sẽ có diện tích bằng nhau.
- Ba đường trung tuyến trong một tam giác cắt nhau tại trọng tâm: Ba đường trung tuyến của tam giác luôn cắt nhau tại một điểm gọi là trọng tâm. Trọng tâm là điểm giao nhau của ba đường trung tuyến, và điểm này chia mỗi đường trung tuyến thành hai phần có tỷ lệ 2:1, với phần gần đỉnh gấp đôi phần gần trung điểm của cạnh.
- Độ dài của đường trung tuyến phụ thuộc vào các cạnh của tam giác: Độ dài của đường trung tuyến trong tam giác có thể được tính thông qua công thức dựa trên các cạnh của tam giác. Công thức tính đường trung tuyến m_a, m_b, m_c giúp tính độ dài của đường trung tuyến đối diện với các cạnh a, b, và c.
- Đặc điểm đối với các loại tam giác: Trong tam giác đều, ba đường trung tuyến trùng với ba đường cao và ba đường phân giác, tức là chúng đồng thời chia tam giác thành các phần đều. Trong các tam giác vuông hay tam giác vuông cân, đường trung tuyến có những đặc điểm riêng về chiều dài và tính chất.
- Đường trung tuyến trong tam giác vuông: Trong tam giác vuông, đường trung tuyến đối diện với cạnh huyền có độ dài bằng nửa độ dài của cạnh huyền.
Các tính chất này giúp đường trung tuyến trở thành một yếu tố quan trọng trong việc phân tích và giải quyết các bài toán hình học liên quan đến tam giác.
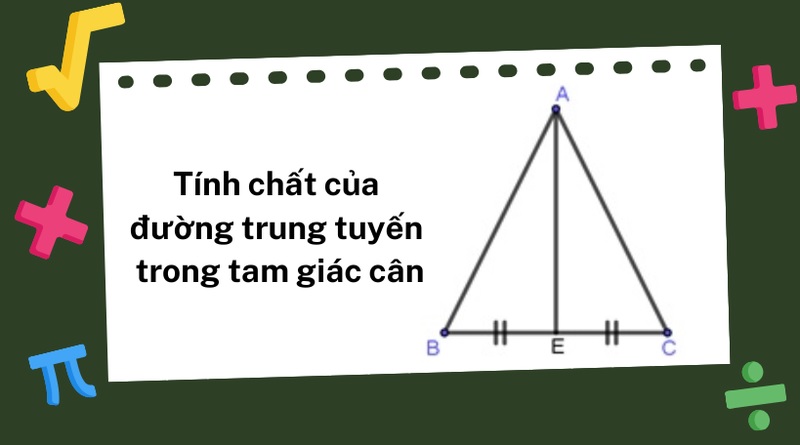Tính chất của đường trung tuyến trong tam giác cânDưới đây là một số bài tập áp dụng đường trung tuyến trong tam giác, giúp bạn củng cố kiến thức và kỹ năng tính toán:
Bài tập 1: Tính độ dài đường trung tuyến
Đề bài: Cho tam giác ABC với các cạnh a = 8, b = 6, c = 10. Tính độ dài của đường trung tuyến mₐ đối diện với cạnh a.
Hướng dẫn giải:
Sử dụng công thức tính độ dài đường trung tuyến mₐ
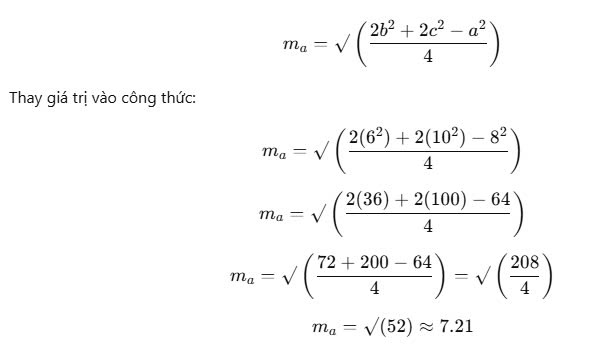
Bài tập 1Kết quả: Độ dài đường trung tuyến mₐ ≈ 7.21 đơn vị.
Bài tập 2: Tính trọng tâm của tam giác
Đề bài: Tam giác ABC có các đường trung tuyến mₐ = 6, mᵦ = 8, m𝑐 = 10. Tính khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác.
Hướng dẫn giải:
Trọng tâm chia mỗi đường trung tuyến thành tỷ lệ 2:1, nghĩa là phần gần đỉnh sẽ dài gấp đôi phần gần trung điểm của cạnh.
bài tập 2Kết quả: Khoảng cách từ trọng tâm đến các đỉnh lần lượt là:
Đỉnh A: 4 đơn vị
Đỉnh B: 5.33 đơn vị
Đỉnh C: 6.67 đơn vị
Bài tập 3: Tam giác vuông và đường trung tuyến
Đề bài: Cho tam giác vuông ABC với AB = 6, AC = 8, BC = 10. Tính độ dài của đường trung tuyến đối diện với cạnh BC (cạnh huyền).
Hướng dẫn giải:
Trong tam giác vuông, đường trung tuyến đối diện với cạnh huyền bằng nửa độ dài của cạnh huyền. Do đó:
mₐ=BC/2=10/2=5
Kết quả: Độ dài của đường trung tuyến đối diện với cạnh huyền BC là 5 đơn vị.
Bài tập 4: Đường trung tuyến trong tam giác đều
Đề bài: Cho tam giác đều ABC với mỗi cạnh có độ dài là 12. Tính độ dài của đường trung tuyến.
Hướng dẫn giải:
Trong tam giác đều, đường trung tuyến trùng với đường cao, và nó chia tam giác thành hai tam giác vuông cân. Ta có công thức tính độ dài đường cao (cũng là đường trung tuyến) trong tam giác đều:
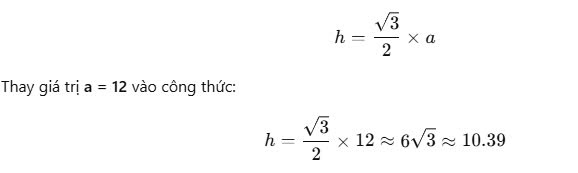
Bài tập 4Kết quả: Độ dài của đường trung tuyến trong tam giác đều là khoảng 10.39 đơn vị.
Bài tập 5: Tính diện tích tam giác nhờ đường trung tuyến
Đề bài: Cho tam giác ABC với đường trung tuyến mₐ = 10, mᵦ = 8, m𝑐 = 6. Tính diện tích của tam giác.
Hướng dẫn giải:
Diện tích của tam giác có thể tính bằng công thức Heron hoặc công thức với đường trung tuyến. Tuy nhiên, bài này yêu cầu sử dụng công thức diện tích tam giác với ba đường trung tuyến:
Bài tập 5Kết quả: Diện tích tam giác là 24 đơn vị vuông.
Những bài tập trên giúp bạn nắm vững cách tính độ dài của đường trung tuyến và áp dụng các tính chất của đường trung tuyến trong các bài toán hình học.
Trên đây chúng tôi đã giải thích chi tiết về đường trung tuyến trong tam giác, các tính chất và công thức tính toán liên quan. Hy vọng bài viết đã mang lại thông tin hữu ích và giúp bạn hiểu rõ hơn về vấn đề này.
Nếu bạn đang tìm kiếm dịch vụ đặt xe taxi sân bay giá rẻ, trọn gói, hãy liên hệ ngay với Nội Bài Vip 24/7 – chuyên cung cấp dịch vụ taxi sân bay uy tín, phục vụ nhanh chóng mọi thời điểm trong ngày.
📞 Hotline: 097.992.3336 | 0865.202.193